La transformation de Kennely (ou transformation étoile-triangle, et inversement) est une méthode mathématique utilisée en électrotechnique pour simplifier l’analyse des réseaux électriques complexes. Elle permet de convertir une configuration de résistances (ou d’impédances) en étoile (Y) en une configuration triangle (Δ), et vice versa, facilitant ainsi les calculs de courants et de tensions dans les circuits.
a) Montage Étoile (Y)
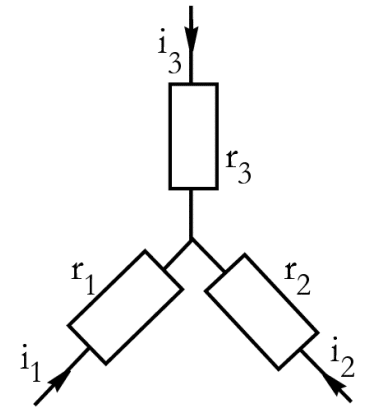
- Trois résistances (r₁, r₂, r₃) sont connectées à un nœud central.
- Utilisé dans les systèmes triphasés (ex. : moteurs électriques).
b) Montage Triangle (Δ)
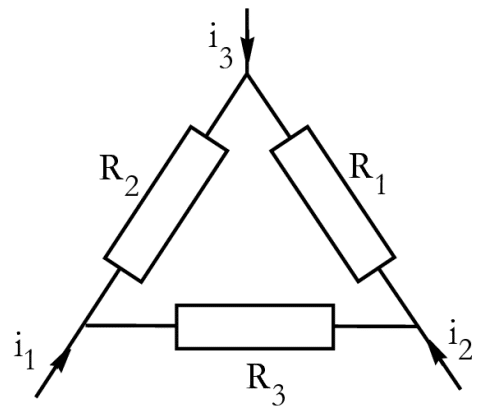
- Trois résistances (R1, R2, R3) sont connectées en boucle fermée.
- Aucun point central.
Problème : Comment convertir un montage en étoile en triangle (et inversement) pour simplifier les calculs ?
Transformations Étoile-Triangle (Y-Δ) et Triangle-Étoile (Δ-Y)
Guide complet avec formules et exemples pratiques pour les techniciens et ingénieurs en électrotechnique.
1. Transformation Étoile vers Triangle (Y → Δ)
Formules de conversion
R1 = r1r2 + r2r3 + r3r1r1
R2 = r1r2 + r2r3 + r3r1r2
R3 = r1r2 + r2r3 + r3r1r3
Exemple pratique
Avec r1 = 2Ω, r2 = 3Ω, r3 = 6Ω :
Numérateur = (2×3) + (3×6) + (6×2) = 6 + 18 + 12 = 36
R1 = 362 = 18Ω
R2 = 363 = 12Ω
R3 = 366 = 6Ω
2. Transformation Triangle vers Étoile (Δ → Y)
Formules de conversion
r1 = R2R3R1+R2+R3
r2 = R1R3R1+R2+R3
r3 = R1R2R1+R2+R3
Exemple pratique
Avec R1 = 18Ω, R2 = 12Ω, R3 = 6Ω :
Dénominateur = 18 + 12 + 6 = 36
r1 = 12×636 = 7236 = 2Ω
r2 = 18×636 = 10836 = 3Ω
r3 = 18×1236 = 21636 = 6Ω
3. Applications pratiques
- Conversion des moteurs triphasés
- Simplification des circuits électriques
- Calcul des impédances équivalentes
Exercice d’application :
Soit le montage suivant :
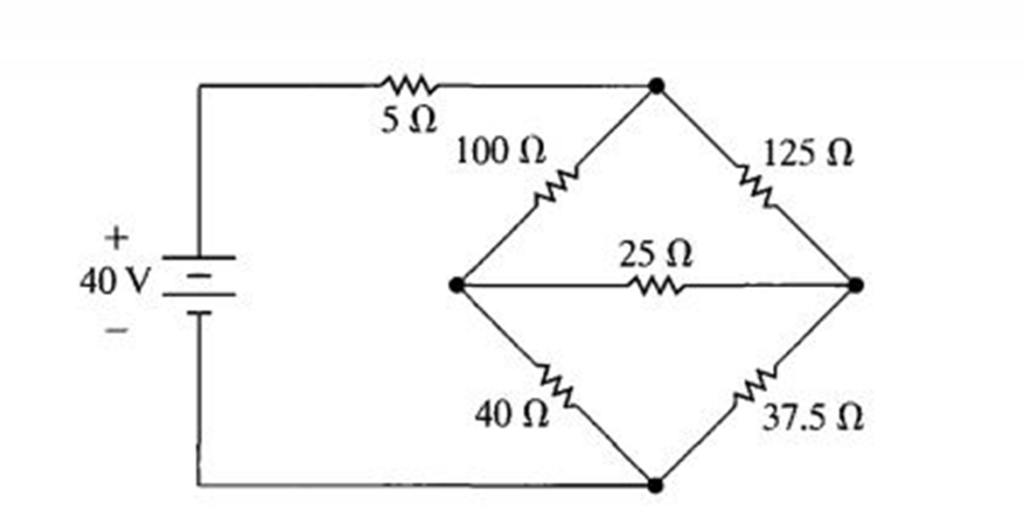
On souhaite déterminer la résistance équivalente du montage.
Nous allons en premier lieu transformer le triangle en étoile
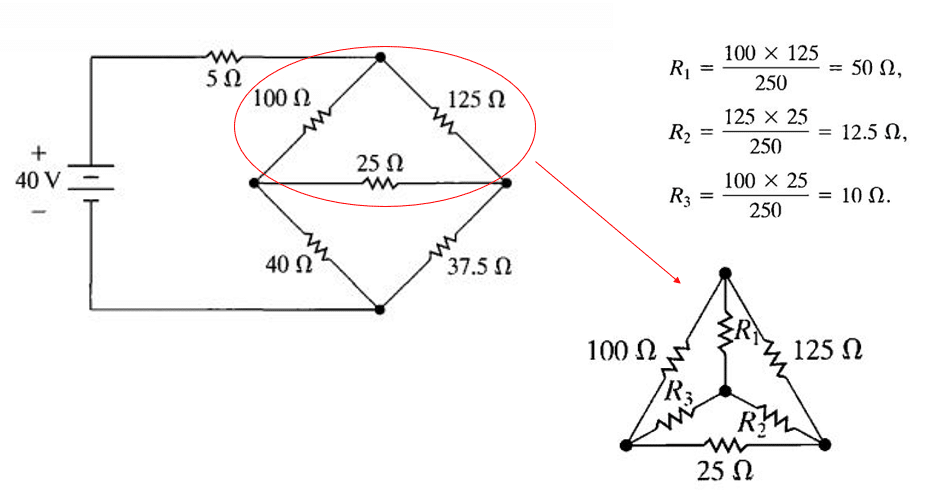
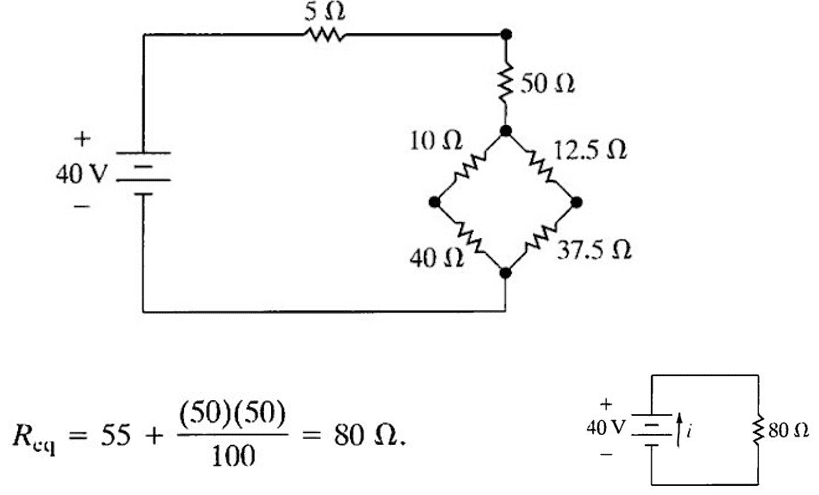
La résistance équivalente donc de ce montage est de 80 Ohms.
Exercice : Pont de Weahtsone
Un pont de Weahtsone est un montage électrique permettant de déterminer une résistance inconnue.
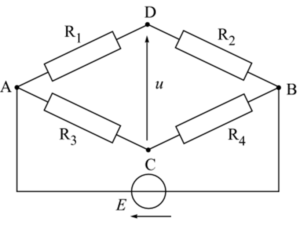
Déterminer la tension u en fonction de E, R1, R2, R3, et R4