Les transformateurs monophasés

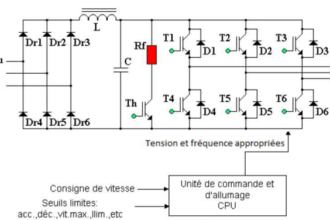
Définition

Un transformateur est un convertisseur « alternatif-alternatif » qui permet de modifier la valeur d’une tension alternative en maintenant sa fréquence et sa forme inchangées.

Le transformateur est un appareil qui peut :

• • Transformer une tension alternative d’une grandeur à une autre grandeur

• • Transformer un courant alternatif d’une grandeur à une autre grandeur

• • Isoler un circuit électrique d’un courant continu circulant dans un autre circuit électrique

• • Faire paraître une impédance comme ayant une autre valeur

Les  transformateurs sont des machines électriques entièrement statiques, cette absence de mouvement est d’ailleurs à l’origine de leur excellent rendement. Leur utilisation est primordiale pour le transport de l’énergie électrique où l’on préfère « transporter des volts plutôt que des ampères ». Ils assurent l’élévation de tension entre la source, et le réseau de transport, puis ils permettent l’abaissement de la tension du réseau vers l’usager.

Transformateur monophasé

Un transformateur monophasé est constitué de 2 bobines en fil de cuivre, l’une dite est dite « primaire », l’autre « secondaire ». Ces bobines sont enroulées sur un noyau magnétique constitué d’un empilage de tôles minces en acier.  Celui-ci permet de relier magnétiquement le primaire et le secondaire en canalisant les lignes de champ magnétiques produites par le primaire.

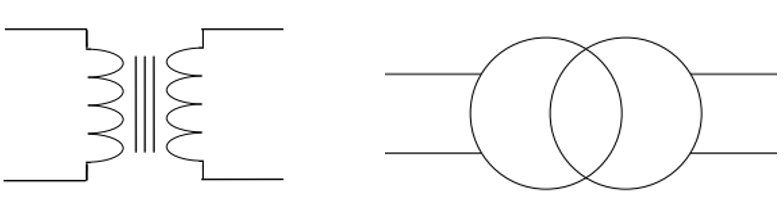
Symboles
On trouve deux symboles.  Sur  celui  à gauche,  les  trois  barres  verticales  symbolise  le  noyau magnétique  qui  permet  à  l’énergie  magnétique  de  passer  du  bobinage  primaire  au  bobinage secondaire.

Principe
Le transformateur est constitué de deux bobines couplées par un noyau de fer conduisant le flux créé par l’une jusqu’au secondaire. Les tensions induites sont proportionnelles aux nombres de spires.

Notations :
On notera d’un indice

• • 1 le primaire

• • 2 le secondaire

• • v ou 0 les grandeurs à vide

• • n les grandeurs nominales

• cc les grandeurs en court-circuit

Le primaire est en convention récepteur alors que le secondaire est en convention générateur.
Les bornes homologues sont telles qu’un courant entrant par celles-ci crée un flux orienté dans le même sens. Les tensions vues sur ces points sont de même polarité.

Remarque :
Il n’y a pas de lien entre la convention choisie et les bornes homologues.
Ceci fait que suivant les auteurs les orientations des vecteurs et tensions peuvent différer.

Relations générales d’un transformateur parfait:

Si on fait rentrer un courant par les bornes homologues, il apparaît une fém e telle que la bobine se comporte comme un générateur.
Toutes les pertes sont négligées : le flux traverse donc les deux bobinages ainsi :
 

   
 

Rapport de transformation

 

avec V₂₀ et V_1N tensions efficaces au primaire et au secondaire et N₁ et N₂ nombres de spires au primaire et au secondaire.

Relation de Boucherot :
Si on suppose que le champ est sinusoïdal alors  
Donc  soit 

 

et 

 avec
Relation sur les courants :

 
Le bilan des puissances est simple :

• P₁ = V₁.I₁.cosj₁ = P₂ = V₂.I₂.cos j₂; et j₁ = j₂
• Q₁ = Q₂ = V₂.I₂.sin j₂ 
• et S₁ = V₁.I₁= V₂.I₂= S_2.

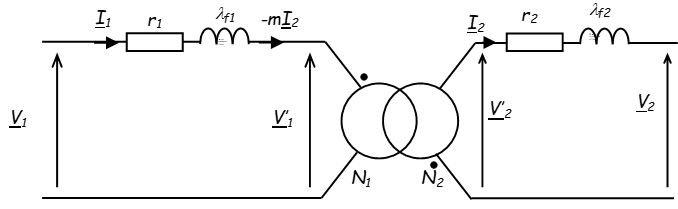
Transformateur réel
Transformateur à vide :
Equations et schéma équivalent
Le transformateur se comporte comme une bobine à noyau de fer :
L’équation des flux donne :

Si l’on considère le courant sinusoïdal ce qui n’est en toute rigueur pas le cas on peut passer aux grandeurs complexes.

 avec  et

• r₁ est la résistance interne de la bobine primaire
• lf1 est l’inductance de fuite primaire
• L_µ est l’inductance magnétisante
• R_F représente les pertes fer

Représentation de Fresnel

Bilan de puissances :
A vide le transformateur absorbe
 
qui mesuré est égal à .
 
qui mesuré est égal à .
Transformateur en charge :
Equations et schéma équivalent

On s’aperçoit alors que le rapport de transformation
Un bilan plus précis des ampères tours

Si l’on ne néglige pas la force magnétomotrice  alors on peut identifier cette perte d’ampère tours à un courant magnétisant que l’on trouve d’ailleurs à vide (le courant secondaire étant nul) :

soit en complexe

donc

Représentation de Fresnel

Bilan de puissances

Transformateur dans l’hypothèse de Kapp :
Simplifications
Dans l’hypothèse de Kapp

alors :
Le rapport des courants est alors tel que
Comme la tension primaire est   alors le rapport des tensions à vide :
L’approximation ainsi faite revient à considérer le schéma équivalent suivant

On remarque que l’on peut toujours introduire les pertes fer par la présence du courant I_µ courant absorbé à vide par le transformateur