Corrigé – Série n°7 Circuits électriques à courant continu

Exercice 1 :

Soit le circuit suivant :

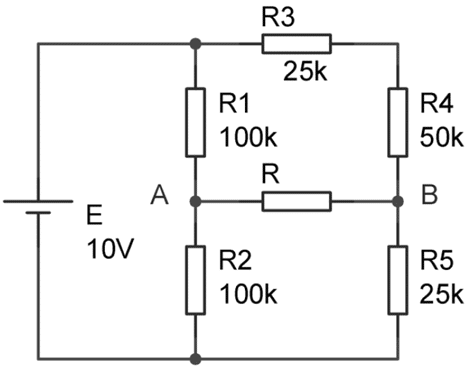
1. Dessiner le modèle équivalent de Thévenin, sans tenir compte de la résistance R.
2. On prend R=100kΩ, calculer la tension aux bornes de la résistance R, ainsi que la puissance dissipée dans celle-ci.

Réponse :

1. Eth  = 2,5V et Rth  = 68,75kΩ
2. I= 14,81µA è UR = 1,48V

Exercice 2 :

Soit le circuit suivant :

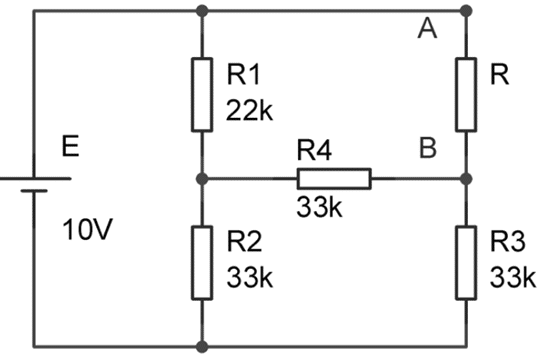
1. Calculer le courant qui circule dans la résistance R = 10kΩ.

Réponse :

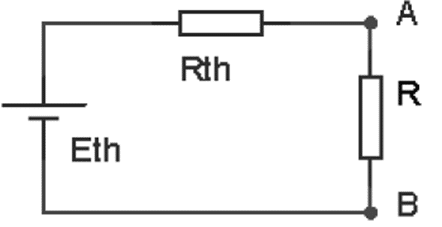
• Eth = 7,5V
• Rth = 19,25kΩ
• I = 256,4µA

Exercice 3 :

On considère le montage ci-dessous :

Lorsque le pont est équilibré, UAB = 0.

On se propose de calculer la résistance R₄ (Capteur) permettant de remplir cette condition.

• 1) Donner l’expression littérale de V_AM en fonction de E, R₁ et R₂
• 2) Donner l’expression littérale de V_BM en fonction de E, R₃ et R₄.
• 3) Donner l’expression littérale de U_AB en fonction de E, R₁, R₂, R₃ et R₄.
• 4) Former la condition d’équilibre : U_AB = 0.
• 5) Donner l’expression littérale de R₄ à l’équilibre en fonction de R₁, R₂ et R₃.
• 6) Calculer la valeur de R₄.

Les données :

• R1 = 10kΩ
• R2 = 1kΩ
• R3 = 2,2kΩ
• R4 = Capteur
• E = 12V

Réponse :

1) Donner l’expression littérale de VAM en fonction de E, R1 et R2

J’applique la loi du pont diviseur de tension : V_AM = (E×R₂)/ (R₁+R₂)

2) Donner l’expression littérale de VBM en fonction de E, R3 et R4.

J’applique la loi du pont diviseur de tension : V_BM = (E×R₄)/ (R₃+R₄)

3) Donner l’expression littérale de U_AB en fonction de E, R1, R2, R3 et R4.

On a V_AM = V_A et V_BM = V_B

U_AB = V_A – V_B = V_AM – V_BM = (E×R₂)/ (R₁+R₂) – (E×R₄)/ (R₃+R₄)

4) Former la condition d’équilibre : UAB = 0.

(E×R₂)/ (R₁+R₂) – (E×R₄)/ (R₃+R₄) = 0

5) Donner l’expression littérale de R4 à l’équilibre en fonction de R1, R2 et R3

On a (E×R₂)/ (R₁+R₂) – (E×R₄)/ (R₃+R₄) = 0

• R₂/ (R₁+R₂) – R₄/ (R₃+R₄) = 0
• R₂/ (R₁+R₂) = R₄/ (R₃+R₄)
• R₂×(R₃+R₄) = R₄×(R₁+R₂)
• R₂×R₃+ R₂×R₄ = R₄×R₁+ R₄×R₂
• R₂×R₃ = R₄×R₁
• R₄ = R₂×R₃/R₁

6) Calculer la valeur de R4.

On a R₄ = R₂×R₃/R₁

Application numérique :

• R₄ = (10³×2.2×10³)/10×10³
• R₄ = 220 Ω

Exercice 4 :

Calculez la capacité totale de :

1. 3 condensateurs en série : 10μF, 10μF et 22μF
2. 4 condensateurs en parallèle : 10pF, 10pF, 33pF et 33pF
3. 2 condensateurs en parallèle (100pF et 220pF) placés en série avec un 3^ème de 220pF

Réponse :

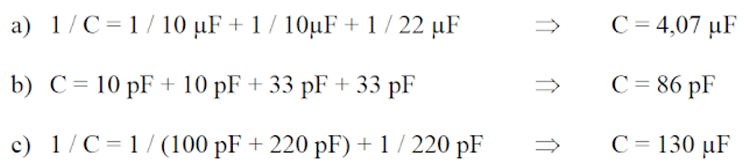
Exercice 5 :

Un condensateur de 100μF est chargé sous une tension de 30V. 

1. Quelle est la quantité Q d’électricité emmagasinée ?
2. Quelle est l’énergie électrique emmagasinée (W) ?

Réponse :

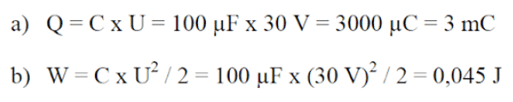
Exercice 6 :

Déterminer la résistance la résistance équivalente vue entre A et B des associations suivantes :

Figure 1 : tous les résistors ont la même résistance R

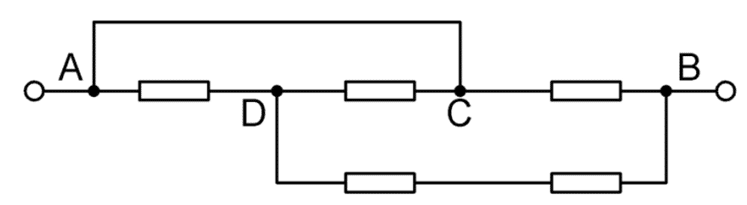
Figure 2

Réponse :

Figure 1 :

• RAB = R//(5R/2) = 5R/7

Figure 2 :

• RAB = R1 + (R2 // R3 // R4) +R5